A. Almashtir va kichraytir!

Xotira: 64 MB, Vaqt: 1000 ms

Masala

Anvarda juda katta son bor. Lekin unga bu son yoqmas edi. U bu sonni kichraytirmoqchi bo'ldi.

U o'z sonini hohlagan marta bu usulda kichraytirishi mumkin:

U hohlagan ikkita sondagi raqamlarni tanlaydi. Agar ularni juftligi (ya'ni 2-ga bo'lgandagi qoldig'i) har hil bo'lsa ularni o'rnini almashtiradi.

Anvar o'z sonining oldida 0 lar turishiga qayg'urmaydi.

Anvar o'z operatsiyalarni qilib bo'lgach, eng minimum qaysi sonni hosil qilishi mumkin?

Kiruvchi ma'lumotlar:

Birinchi qatorda Anvarning soni beriladi, uning uzunligi \(1\) dan \(2 × 10⁵\) gacha bo'lishi mumkin.

Chiquvchi ma'lumotlar:

Anvar olishi mumkin bo'lgan eng kichik son.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	50	05
2	642	642

B. Mandarinlar

Xotira: 32 MB, Vaqt: 1000 ms

Masala

Temur mandarinlarni juda yaxshi ko'radi va uyga qaytvotganda aynan k dona mandarin sotib olmoqchi. Uning yo'li bo'ylab n ta magazin bor, va har bir magazinda:

i-magazinda \(a_i\) ta mandarin mavjud, har biri \(p_i\) so‘mdan sotiladi.

Temur juda sodiq xaridor, shuning uchun u barcha k dona mandarinni bitta magazindan sotib olmoqchi. Lekin uni ko'p pul ketqizish niyati ham yo'q. Temurga k dona mandarinni minimal narxda sotib olish uchun yordam bering yoki bu mumkin emasligini aniqlang.

Kiruvchi ma'lumotlar:

Birinchi qatorda ikki butun son n va k \(( 1 ≤ n, k ≤ 10^5 )\) - magazinlar soni va Temur sotib olmoqchi bo‘lgan mandarinlar soni.
Ikkinchi qatorda n ta butun son \(a_1, a_2, ..., a_n ( 1 ≤ a_i ≤ 10^9 )\) — har bir magazindagi mandarinlar soni.
Uchinchi qatorda n ta butun son \(p_1, p_2, ..., p_n ( 1 ≤ p_i ≤ 10^9 )\) — har bir magazin uchun bir dona mandarinning narxi.

Chiquvchi ma'lumotlar:

Yagona butun sonni chiqaring — Temur k dona mandarinni sotib olishi uchun kerak bo‘lgan minimal pul summasi yoki agar bu mumkin bo‘lmasa, -1 sonini chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	10 3 46 25 33 12 17 66 26 3 7 96 46 37 61 6 22 64 89 82 20 10	18

C. Mandarinni qo'yib tur! #1

Xotira: 32 MB, Vaqt: 1000 ms

Masala

Anvarjon akasini mandarinlar bilan magazindan qaytayotganini koʻrib, mandarin soʻradi. Ammo akasi:
"Mandarinni vazifalaringni tugatib olasan," dedi.

Anvarjon barcha masalalarni yechib boʻlgandi, faqat bitta qolgandi:

Sizga \(n\) uzunlikdagi \(a\) massivi beriladi. Shu massivda qandaydir \(k\) uzunlikdagi barcha ketma-ket (contiguous) submassivlarning summasi o'zaro teng boʻlishi kerak.

Sizdan talab qilinadi:
Nechta shunday \(k\) qiymati borligini aniqlang!

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n(1≤n≤2·10^3)\) soni kiritiladi.

Ikkinchi qatorda \(n\) ta \(a\) massivi elementlari \(aᵢ(1≤aᵢ≤10^9)\) kiritiladi.

Chiquvchi ma'lumotlar:

Masala shartiga tog'ri keladigan \(k\) qiymatiga teng bo'la oladigan sonlar sonini chop eting.

Izoh:

Birinchi testdagi \(k\) qiymatlari: \([10]\)

Ikkinchi testdagi \(k\) qiymatlari: \([14,20]\)

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	10 1 1 9 9 7 2 4 6 9 2	1
2	20 4 9 4 9 7 3 9 2 2 9 10 8 6 1 4 9 4 9 7 3	2

D. Yo'qmi?

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Anvarjon barcha masalalarni yechib bo'ldim deb quvoniyatganida bittasini bayqamay qolganini ko'rib qoldi. U buni ko'rib hafa bo'lib qoldi va umuman masala yechgisi kelmay qoldi. Lekin bu masalani yechish juda muhim edi, shunga siz urinib ko'ring.

Masala sharti quydagicha edi:

Sizga \(n\) uzunlikdagi \(a\) massivi beriladi. Siz ular orqali \(q\) ta savolga javob berishingiz kerak.

Savollar quydagi \(2\) ta turda bo'lar edi:

\(1 i v\) - Siz massivni \(i\) - elementini \(v\) ga almashtirishingiz kerak.
\(2\) - Siz massivda yo'q bo'lgan va \([1,10^9]\) oralig'ida bo'lgan barcha sonlar yig'indisini chop etishingiz kerak.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n\) va \(q\) \((1≤n,q≤2*10^5)\) sonlari kiritiladi.

Ikkinchi qatorda \(n\) ta \(a\) massivi elementlari \(aᵢ(1≤aᵢ≤10^9)\) kiritiladi.

Keyingi \(q\) ta qatorda \(2\) hil turda:

\(1 i v (1≤i≤n, 1≤v≤10^9)\) sonlari kiritiladi.
\(2\) soni kiritiladi.

Chiquvchi ma'lumotlar:

Har bir \(2\) - turdagi savol uchun javobni chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	1 1 7 2	500000000499999993
2	2 5 16 59 1 1 61 1 1 59 1 1 9 1 1 33 2	500000000499999908

E. Qo'shishni ham bilmaysanmi?

Xotira: 32 MB, Vaqt: 1000 ms

Masala

Anvar qo'shish amalini endi o'tgan edi… Shunga unda bir ikkita xatolik ketadi. Aynan u o'tkazish jarayonida 1 ta xonaga emas, 2 tasiga o'tkazib yuboradi.

Masalan \(2039+2976\) ni oddiy hisoblashda:

Anvarni hisoblashida:

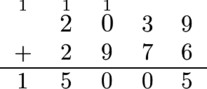
Sizga \(a\) va \(b\) sonlari summasini topish juda oson tuyilish mumkin. Shunga men masalani qiyinlashtirdim. Aynan siz \(a+b=n\)va \(1≤a,b≤n\) bo'ladigan \((a,b)\) juftliklar sonini topishingiz kerak!

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n(1≤n≤10^{18})\) soni kiritiladi.

Chiquvchi ma'lumotlar:

Birinchi qatorda \(a+b=n\) bo'ladigan \((a,b)\) juftliklar sonini chop eting.

Izoh:

Birinchi testdagi juftliklar \(1+9, 2+8, 3+7, 4+6, 5+5, 6+4, 7+3, 8+2\) yoki \(9+1\) bo'la oladi.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	100	9
2	19	18
3	1	0
4	3	2
5	6	5

F. Ez or not?

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Sizda \(n\) uzunlikdagi \([1,2,3,…,n]\)

massivi bor. Siz massivdagi summasi \(m\) ga bo'lgandagi qoldig'i \(k\) ga teng bo'lgan qism to'plamlar sonini topishingiz kerak.

Qism to'plam - massivdan bir-nechta(0 ham bo'lishi mumkin) element o'chirgandan so'ng paydo bo'ladigan to'plam.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(t(1≤t≤10^5)\) - testlar soni beriladi.

Keyingi \(t\) ta qatorda \(n, m, k(1≤n≤10^4, 1≤k<m≤30)\) - sonlari kiritiladi.

Chiquvchi ma'lumotlar:

\(t\) ta qatorda massivdagi summasi \(m\) ga bo'lgandagi qoldiq \(k\) ga teng bo'lgan qism to'plamlar sonini \(10^9+7\) ga bo'lgandagi qoldig'ini chop eting.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	10 6 6 3 8 4 1 3 1 0 10 5 4 7 4 1 8 10 8 5 4 2 4 8 0 6 7 5 4 3 1	12 64 8 204 32 26 8 2 9 6

G. Yo'qmi? #2

Xotira: 256 MB, Vaqt: 2000 ms

Masala

Anvarjon barcha masalalarni yechib bo'ldim deb quvoniyatganida bittasini bayqamay qolganini ko'rib qoldi. U buni ko'rib hafa bo'lib qoldi va umuman masala yechgisi kelmay qoldi. Lekin bu masalani yechish juda muhim edi, shunga siz urinib ko'ring.

Masala sharti quydagicha edi:

Sizga \(n\) uzunlikdagi \(a\) massivi beriladi. Siz ular orqali \(q\) ta savolga javob berishingiz kerak.

Savollar quydagi \(2\) ta turda bo'lar edi:

\(1 i v\) - Siz massivni \(i\) - elementini \(v\) ga almashtirishingiz kerak.
\(2 l r\) - Siz massivda yo'q bo'lgan va \([l,r]\) oralig'ida bo'lgan barcha sonlar yig'indisini chop etishingiz kerak.

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n\) va \(q\) \((1≤n,q≤2*10^5)\) sonlari kiritiladi.

Ikkinchi qatorda \(n\) ta \(a\) massivi elementlari \(aᵢ(1≤aᵢ≤2*10^5)\) kiritiladi.

Keyingi q ta qatorda 2 hil turda:

\(1 i v (1<=i<=n, 1<=v<=2*10^5)\) sonlari kiritiladi.
\(2 l r (1<=l<=r<=2*10^5)\) soni kiritiladi.

Chiquvchi ma'lumotlar:

Har bir \(2\) - turdagi savol uchun javobni chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	2 1 5 4 2 2 4	5
2	6 6 8 7 10 5 3 2 1 3 10 1 5 1 1 5 1 1 5 3 1 1 8 2 1 3	1

H. Mandarinni qo'yib tur! #2

Xotira: 256 MB, Vaqt: 1000 ms

Masala

Anvarjon akasini mandarinlar bilan magazindan qaytayotganini koʻrib, mandarin soʻradi. Ammo akasi:
"Mandarinni vazifalaringni tugatib olasan," dedi.

Anvarjon barcha masalalarni yechib boʻlgandi, faqat bitta qolgandi:

Sizga \(n\) uzunlikdagi \(a\) massivi beriladi. Shu massivda qandaydir \(k\) uzunlikdagi barcha ketma-ket (contiguous) submassivlarning summasi teng boʻlishi kerak.

Sizdan talab qilinadi:
Nechta shunday \(k\) qiymati borligini aniqlang!

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n(1≤n≤2·10^5)\) soni kiritiladi.

Ikkinchi qatorda \(n\) ta \(a\) massivi elementlari \(aᵢ(1≤aᵢ≤10^9)\) kiritiladi.

Chiquvchi ma'lumotlar:

\(k\) qiymatiga teng bo'la oladigan sonlar sonini chop eting.

Izoh:

Birinchi testdagi \(k\) qiymatlari: \([10]\)

Ikkinchi testdagi \(k\) qiymatlari: \([14,20]\)

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	10 1 1 9 9 7 2 4 6 9 2	1
2	20 4 9 4 9 7 3 9 2 2 9 10 8 6 1 4 9 4 9 7 3	2

I. nidtamasI ning sevimli massivi #2

Xotira: 256 MB, Vaqt: 2000 ms

Masala

Bu masala nidtamasI ning sevimli massivi masalasining modifikatsiyasi. Masalalarni yechish uslubi har hil, shunga birinchisini yechish muhim emas.

nidtamasI da \(n\) uzunlikdagi \(a\) massivi bor edi. U o'z massivini zo'r deb hisoblardi, lekin u uni \(q\) ta operatsiya orqali judayam zo'r qilmoqchi! U har bir operatsiyada 2 hil turdagi operatsiyadan bittasini bajaradi:

\(1 l r\) sonlarini tanlab, har bir \(i(l≤i≤r)\) uchun \(a\) massivining \(i\) - elementiga \((i-l+1)\) sonini qo'shadi, yani \(a[i]:=a[i]+(i-l+1)\) qiladi!
\(2 i\) a massivining \(i\) - elementini chop etadi yani \(a[i]\) ni chop etadi.

Siz ham shu operatsiyalarni bajaring!

Kiruvchi ma'lumotlar:

Birinchi qatorda \(n,q(1≤n,q≤2*10^5)\) sonlari kiritiladi.

Ikkinchi qatorda \(n\) ta \(aᵢ(1≤aᵢ≤10^6)\) soni kiritiladi.

Keyingi \(q\) ta qatorda 2 hil turdagi operatsiya:

\(1 l r (1≤l≤r≤n)\).
\(2 i (1≤i≤n)\).

Chiquvchi ma'lumotlar:

Har bir \(2\) - turdagi operatsiya uchun \(a[i]\) ni chiqaring.

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	5 6 3 3 1 1 3 2 5 2 4 2 2 1 2 4 1 4 5 2 4	3 1 3 5
2	5 9 22 8 23 21 4 1 1 2 1 5 5 1 2 2 1 4 5 1 1 3 2 5 2 5 1 3 5 2 3	7 7 27

J. Bo'rilar va qo'ylar

Xotira: 32 MB, Vaqt: 1000 ms

Masala

Bir kuni Odilga \(m\) echkini va \(m\) bo'ri bir daryodan o'tkazish kerak edi. Qayiq \(n\) jonivorni va Odilni olib o'ta oladi. Agar biror joyda bo'rilar echkilardan ko'proq bo'lsa, bo'ri echkilarni yeyadi(qayiqda ham). Hohlagan paytda qayiqda kamida bir jonivor olib ketishi kerak. Qayiq qirg'oqka yetgach, barcha jonivorlar tushadi va Odil tanlagan jonivorlar qayiqka o'tiradi. Odil hamma jonivorlarni xavfsiz o'tkazib, xafa bo'lmasligi kerak. Nechta marta qayiqdan foydalanish kerak?

Kiruvchi ma'lumotlar:

Birinchi qatorda ikkita butun son \(m\) va \(n(1≤m,n≤10^5)\) berilgan — jonivorlar soni va qayiqning sig'imi.

Chiquvchi ma'lumotlar:

Agar barcha jonivorlarni hech kim xafa bo'lmasdan va barcha mallalar omon qolgan holda o'tkazib bo'lmasa, \(-1\) ni chiqaring. Aks holda, bir butun sonni chiqaring — daryoni necha marta o'tish kerakligini.

Izoh:

Birinchi test xato! Bu holatda \(-1\) chiqishi kerak deydiganlar uchun: Bu test tog'ri va buni yechish ham mumkin!

Unda bizga testni tushintirib bering:
Unda masalani qizig'i qolmaydi!

Misollar:

#	INPUT.TXT	OUTPUT.TXT
1	3 2	11
2	33 3	-1