A. Boshliqlik sindromi
Xotira: 32 MB, Vaqt: 1000 msRobolandiyada bir tashkilot bor. U tashkilotning ofislari n × m o‘lchamli jadval shaklida joylashgan bo'lib, har bir ofisning ichki devori quyidagi ranglardan biri bilan bo‘yalgan:

- A → Amethyst (binafsha)
- B → Beige (Sarg'ish)
- C → Coral (Marjonrang)
- D → Denim (jeans ko‘ki)
Ofislarning har biri to‘rt tomondan qo‘shnilari bilan eshik orqali tutashgan (chap, o‘ng, yuqori, past).
Yaqinda bu tashkilotga yangi rahbar tayinlandi. Unda “boshliqlik sindromi” bor:
- U qaysi ofisga kirsa ham, albatta kamchilik topadi va devorlarni boshqa rangga bo‘yashni buyuradi. Ya’ni, har bir ofisning rangi o‘zgarishi kerak va yangi rang eski rangdan farq qilishi shart.
- Bundan tashqari, rahbarning yana bir qat’iy talabi bor: qo‘shni ikki ofisning rangi bir xil bo‘lishi mumkin emas.
Sizning vazifangiz
Ofislarning ranglarini qayta tanlang:
- Qayta tanlangan rang A, B, C yoki D bo'lishi kerak.
- Har bir ofisning yangi rangi eski rangidan farq qilishi kerak.
- Yonma-yon (qo'shni) ofislarning ranglari bir xil bo‘lmasligi kerak.
Kirish faylining dastlabki satrida ikkita butun son n va m \((1 \le n, m \le 500)\) — qator va ustunlar soni kiritiladi.
Keyingi n ta qatorning har birida m ta belgi (A, B, C, D) — hozirgi ranglar jadvali kiritiladi.
Agar ofislarni qayta bo'yashning imkoni bo'lsa n ta qatorda, har birida m ta belgi — yangi ranglar jadvalini chop eting. Aks holda IMPOSSIBLE yozuvini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 4 ADAD DDDD DDBC AACD |
CBDC ACBA BACD DBAC |
B. Passportlar
Xotira: 128 MB, Vaqt: 2000 msRobolandiya mamlakatida \(N\) ta shahar mavjud. Shaharlar orasida \(N-1\) ta ikki yo‘nalishli yo‘l qurilgan. Bu yo‘llar shunday ulangan-ki, har qanday shahardan boshqasiga bevosita yoki bir nechta shaharlar orqali borish mumkin (ya’ni, graf daraxt shaklida).
Har bir yo‘l ikki shaharning orasini bog‘laydi va uning ustida \(W_{i}\) soni yozilgan. Qo‘shni shaharlar deb, orasida bevosita yo‘l mavjud bo‘lgan shaharlar juftligiga aytamiz. Agar kimdir bir shahardan uning qo‘shnisiga o‘tmoqchi bo‘lsa, uning pasport kuchi kamida shu yo‘l qiymatiga (\(W_{i}\)) teng bo‘lishi kerak. Kuch qiymati \(w\) bo‘lgan pasport aynan \(w\) tangaga tushadi.
Shunday qilib, ikki shahar \(a\) va \(b\) orasida sayohat qilish uchun pasport kuchi marshrutdagi eng katta \(W_{i}\) qiymatiga teng bo‘lishi kifoya. Ya’ni, siz tanlagan yo‘ldagi yo‘llar orasidagi maksimal qiymatni qoplash zarur.
Sizning vazifangiz: barcha juftliklar uchun \((1 \le i < j \le N)\) sayohat qilish uchun zarur bo‘lgan minimal pasport narxini hisoblang va ularning yig‘indisini toping.
Birinchi qatorda bitta butun son \(N\) (\(1 \le N \le 2 \times 10^{5}\)) — shaharlar soni.
Keyingi \(N-1\) qatorda uchta butun son \(a, b, W\) (\(1 \le W \le 10^{6}\)) beriladi — bu \(a\) va \(b\) shaharlari orasida qiymati \(W\) bo‘lgan yo‘l mavjudligini bildiradi.
Bitta butun son chiqaring — barcha \(\frac{N(N-1)}{2}\) juftlik uchun minimal pasport narxlari yig‘indisi.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 1 2 5 2 3 1 2 4 2 |
20 |
C. Renessansdagi birinchi kun
Xotira: 32 MB, Vaqt: 1000 msRenessans oromgohiga kelgandan keyin Nurbaxsh va Husanboy do'konga chiqib ichimlik olib kelishga qaror qilishdi.
Ular borgan do'konda \(n\) xil gazli va \(m\) xil gazsiz ichimlik bor ekan. Nurbaxsh va Husanboy bittadan ichimlik olishmoqchi. Ularni qiziqtirgan savol: Ular necha xil usulda do'kondan har biri bittadan (jami bo'lib 2 ta) ichimlik olishlari mumkin?
Ularga bu savolga javob topishga yordam bering.
Yagona qatorda ikkita butun son \(n\) va \(m\) , mos ravishda do'kondagi gazli va gazsiz ichimlik turlari sonlari, kiritiladi.
\((1\leq n, m \leq10^9)\)
Yagona qatorda nechi xil usulda ichimlik olishlari mumkinligini chiqaring.
Namuna testi uchun izoh:
1 turdagi gazli ichimlik va 1 turdagi gazsiz ichimlik bor ekan.
Gazli ichimlik: Pepsi, gazsiz ichimlik Tropik bo'lsin.
Jami bo'lib 4 xil usulda ichimlik olishlari mumkin:
- Pepsi, Tropik
- Pepsi, Pepsi
- Tropik, Pepsi
- Tropik, Tropik
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 1 |
4 |
D. AYOQSH
Xotira: 32 MB, Vaqt: 1000 msIkrom uzunligi \(10^9\) km dan iborat bo'lgan yo'lning \(D\) - kmligida yashaydi. Bu yo'lning har \(A\) km ligida (ya'ni, 0, A, 2A, 3A, ...) Ibr ga tegishli AYOQSH mavjud, har \(B\) km ligida Carvon ga tegishli AYOQSH mavjud, hamda har \(C\) km ligida DipOil ga tegishli AYOQSH mavjud.
Eslatma: Bir nuqtada bir nechta turdagi AYOQSH lar bo'lishi mumkin, masalan 0-kmlikda barcha turdagi, ya'ni Ibr, Carvon va DipOil ga tegishli AYOQSH lar bor.
Ikrom o'zining avtomobiliga yoqilg'i quyish uchun uyidan chiqdi, hamda uyiga eng yaqin masofada joylashgan AYOQSH ga borishga qaror qildi. Agar eng yaqin joylashgan AYOQSH lar soni 1 tadan ko'p bo'lsa Ikrom qaysi AYOQSH ga borishni tanlashda qiynalib qoladi.
Ikromga eng yaqinda joylashgan AYOQSH gacha bo'lgan masofani topishda yordam bering. Agar eng yaqin joylashgan AYOQSH lar soni bittadan ko'p bo'lsa Ikromga "Istaganingizni tanlashingiz mumkin!" degan xabarni yetkazing.
Kirish faylining dastlabki satrida bitta butun son, \(T(1 \le T \le 10)\) testlar soni. Keyingi \(T\) ta qatorning har birida to'rttadan butun son, \(A, B, C, D( 1 \le A, B, C, D \le 10^9)\) sonlari kiritiladi.
Har bir test uchun alohida qatorda so'ralgan javobni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 5 14 11 29 23 10 21 35 |
1 Istaganingizni tanlashingiz mumkin! 5 |
E. Nurlar soni
Xotira: 64 MB, Vaqt: 2000 msNyuboy matematikani o'rganishni boshladi, u koordinatalar sistemasiga juda qiziqadi. U koordinatalar sistemasida nuqtalardan foydalanib kvadrat yasashni yoqtiradi. Nyuboy o'lchami \(N \times N\) bo'lgan kvadrat yasamoqchi bo'lsa, \(0\le x \le N\) va \(0\le y \le N\)shartni qanoatlantiradigan barcha butun koordinatalarga nuqta qo'yib chiqadi.
Nyuboy bugun matematika darsida “Nur” bilan tanishdi.
Nur - bir tomoni chegaralangan va ikkinchi tomoni cheksiz ketuvchi geometrik shakl.
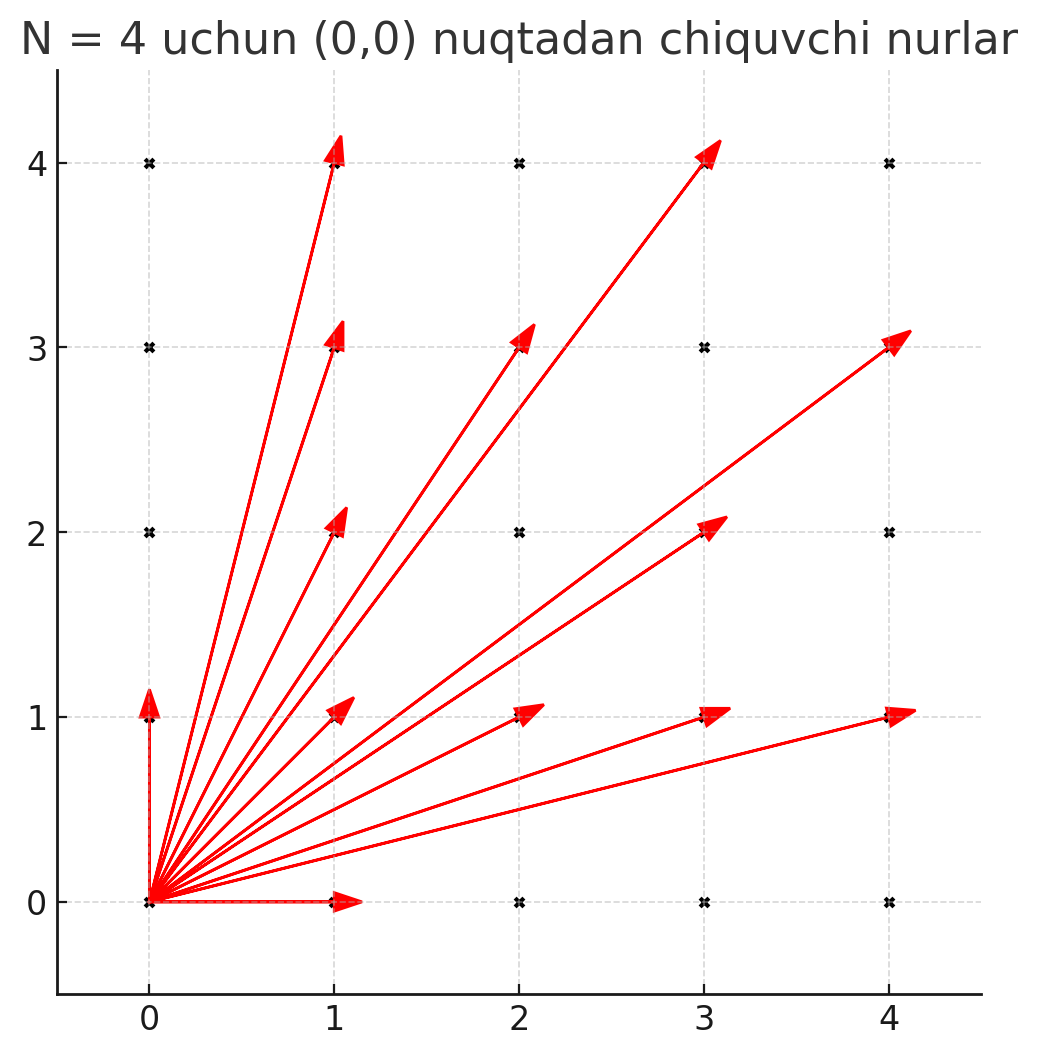
Nyuboy boshlanish nuqtasi \((0,0)\) da joylashgan hamda yo'nalishi o'zi yasagan \(N \times N\) o'lchamli kvadratning \((0,0)\) nuqtasidan tashqari har bir nuqtasiga qaratilgan Nurlar chiza boshladi, bunda u bir Nur ni takroran chizmaydi.
Nyuboy barcha Nurlarni chizib bo'lgach, u yerda jami nechta Nur chizilganligiga qiziqib qoldi. \(N\) ning kichik qiymatlari uchun buni aniqlash Nyuboyga qiyinchilik tug'dirmaydi, ammo \(N\) ning katta qiymatlarida natijani aniqlash uchun Nyuboydan juda ko'p vaqt talab qilinadi. Shu sababli Nyuboy siz dasturchilardan yordam so'ramoqchi. U sizga o'zi yasagan kvadratning tomon uzunligi \(N\) ni aytadi, siz esa unga nechta Nur o'tkazish mumkinligini aytishingiz kerak.
Kirish faylining yagona satrida bitta butun son, \(N (1 \le N \le 10^5)\)soni kiritiladi.
Chiqish faylida yagona butun son, Nyuboyning kvadratidagi nuqtalarga qaratib chizilgan Nurlar sonini chop eting.
1 - test uchun tushuntirish
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
4 |
13 |
| 2 |
1 |
3 |
F. Raqamli pechenyelar
Xotira: 32 MB, Vaqt: 1000 msAzizbek sehrli raqam-pechenyelarni bir-biriga ulab, ulardan bir katta butun son yasadi. Endi u ushbu son ustida quyidagicha o‘yin o‘ynaydi:
- Har qadamda aniq bitta raqamni (istalgan joydan) o‘chirib tashlaydi.
- O‘chirilgan raqamdan so‘ng qolgan raqamlar bir-biriga yopishib, tartibi saqlanadi.
- Agar raqamlarning boshida nol(lar) paydo bo‘lsa, ularni birdan olib tashlaydi (ya’ni, oldinda nol raqami qolmaydi).
- Har safar yangi hosil bo‘lgan son tub son bo‘lsa, o‘yin davom etadi. Agar tub bo‘lmasa, o‘yin shu zahoti to‘xtaydi.
Boshlang‘ich son ham hisobga olinadi: agar tub bo‘lsa, o‘zi ham birinchi holat sifatida qabul qilinadi.
Shunday tartibda raqamlarni o‘chirish ketma-ketligini eng zo‘r tanlab, Azizbek eng ko‘p necha marta tub son bilan uchrashishi mumkinligini (boshlang‘ich holat ham qo‘shiladi) aniqlang.
Sizning vazifangiz: Berilgan son \(N\) uchun yuqoridagi o‘yinda raqamlarni qanday ketma-ketlikda o‘chirish mumkinligi ichida, ketma-ket tub sonlar maksimal sonini chiqaring.
Yagona qatorda natural son - \(N\) beriladi
\(1 \le N \le 10^9\)
Bitta butun son chiqaring — jarayon davomida ketma-ket tub sonlar maksimal sonini.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
11 |
1 |
| 2 |
2 |
1 |
| 3 |
773 |
3 |
| 4 |
300007 |
2 |
| 5 |
15 |
0 |
G. Sheldonning sevimli o‘yini
Xotira: 32 MB, Vaqt: 1000 ms
Eslatma: O'yinning asl nomi “Rock, Paper, Scissors, Lizard, Spock”, bu o'yin The Big Bang Theory ko'rsatuvi yordamida Sheldon tomonidan ommalashtirilgan bo'lganligi sababli uni Sheldon's game deb atashadi.
Husanboy va Nurbaxsh "Umumiy o'rta ta'lim tashkilotlarida faoliyat ko'rsatayotgan informatika va axborot texnologiyalari fani o'qituvchilari o'rtasida Respublika olimpiadasi"ning final bosqichiga hakamlik qilish uchun lagerga kelishdi.
Musobaqaning 1-kuni ishtirokchilar uchun juda qiziqarli bo'ldi, chunki ular bir-biridan qiziqarli bo'lgan masalalar ishlashdi. Husanboy va Nurbaxsh musobaqada ishtirok etmagan bo'lsada musobaqaning birinchi kuni ular uchun ham qiziqarli bo'ldi. Bunga sabab Husanboy va Nurbaxsh vaqtlarini qiziqarli o‘tkazish uchun “Rock, Paper, Scissors, Lizard, Spock” o‘yinini o‘ynashga qaror qilishdi.
O‘yin quyidagi qoidalarga ega:
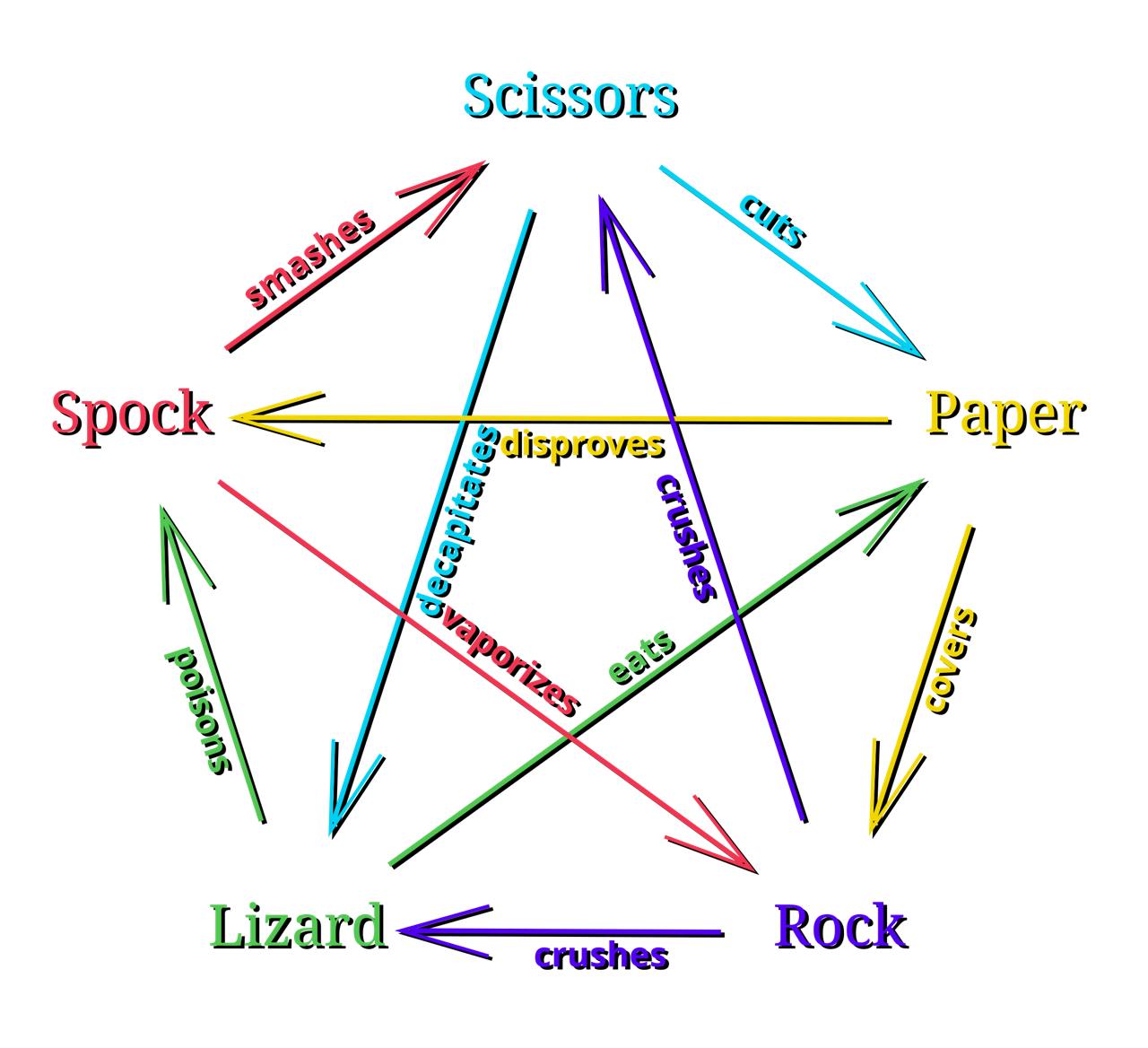
- Scissors kesadi Paperni
- Paper qoplaydi Rockni
- Rock ezadi Lizardni
- Lizard zaharlaydi Spockni
- Spock sindiradi Scissorsni
- Scissors chopib tashlaydi Lizardni
- Lizard yeydi Paperni
- Paper rad etadi Spockni
- Spock bug‘laydi Rockni
- Rock sindiradi Scissorsni
Har bir raundda Husanboy va Nurbaxsh bittadan belgi tanlaydi. Agar Husanboyning belgisi Nurbaxshniki ustidan g‘alaba qozonsa, bu raundni Husanboy yutadi. Agar Nurbaxshning belgisi Husanboyniki ustidan g‘alaba qozonsa, bu raundni Nurbaxsh yutadi. Agar ikkovi bir xil belgi tanlasa, bu raund natijasi durang bo‘ladi.
Sizga Husanboy va Nurbaxsh jami necha marotaba o'yin o'ynaganligi soni \(N\) va har bir raunddagi ikkala o‘yinchining tanlovi beriladi.
Sizning vazifangiz quyidagilarni aniqlash:
- Husanboy nechta g‘alaba qozondi?
- Nurbaxsh nechta g‘alaba qozondi?
- O'yin natijasi necha marotaba durang bo‘ldi?
Kirish faylining dastlabki satrida bitta butun son, \(N(1 \le N \le 10^5)\) soni, jami o'ynalgan raundlar soni kiritiladi.
Keyingi \(N\) ta satrda bo'sh joy bilan ajratilgan holda ikkita belgi, Husanboy va Nurbaxshning tanlovi kiritiladi.
Tanlov belgilari quyidagilarni anglatadi. S - Scissors, P - Paper, R - Rock, L - Lizard, K - spocK
Chiqish faylining yagona satrida uchta butun son:
- Husanboy nechta g‘alaba qozondi?
- Nurbaxsh nechta g‘alaba qozondi?
- O'yin natijasi necha marotaba durang bo‘ldi?
savollariga javobni chop eting.
- 1-raund: Rock > Scissors → Husanboy g‘alaba qozondi
- 2-raund: Lizard > Spock → Husanboy g‘alaba qozondi
- 3-raund: Spock > Rock → Husanboy g‘alaba qozondi
- 4-raund: Paper = Paper → durang
- 5-raund: Lizard < Scissors → Nurbaxsh g‘alaba qozondi
Natija: Husanboy 3, Nurbaxsh 1, durang 1.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 R S L K K R P P L S |
3 1 1 |
H. Jozibali subsequence
Xotira: 128 MB, Vaqt: 1000 msSizga uzunligi \(N\) ga teng bo'lgan, butun sonlardan iborat \(A\) massiv berilgan. Sizning vazifangiz massivdagi jozibali subsequencelar sonini sanashdan iborat.
Subsequence - massivdan 0 yoki bir nechta elementni o'chirishdan hosib bo'ladigan ketma-ketlik.
Masalan [2,1,3] ketma-ketlikda 8 ta har xil subsequence bor, bular: [], [2], [1], [3], [2,1], [2,3], [1,3], [2,1,3].
Massivning turli o'rinlaridagi elementlarni o'chirishdan hosil bo'ladigan subsequence lar turlicha subsequence hisoblanadi. Masalan [2,2,3] ketma ketlikda ham 8 ta har xil subsequence bor, bular: [], [2] (2-element), [2] (3-element), [3], [2,2], [2,3](1 va 3 - element), [2,3] (2 va 3-element) , [2,2,3]
Jozibali subsequence - quyidagi shartlarning barchasini qanoatlantiradigan subsequence ga aytiladi:
- Elementlar soni kamida 2 ta bo'lgan subsequence;
- Elementlari qiymati bo'yicha aynan o'sish tartibida joylashgan subsequence;
- Ketma-ket kelgan ixtiyoriy 2 elementi orasidagi farq juft son bo'lgan subsequence.
Kirish faylining birinchi satrida bitta butun son, \(N(1 \le N \le 2 \times 10^5)\) - \(A\) massiv elementlari soni kiritiladi. Ikkinchi satrda \(N\) ta butun son, \(A (1 \le A_i \le 10^9)\) massiv elementlari kiritiladi.
\(A\) massivda jami nechta jozibali subsequence mavjudligini aniqlang va natijani \(10^9+9\) ga bo'lgandagi qoldiqni chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
10 20 6 18 10 4 20 10 18 4 2 |
17 |
| 2 |
10 4 3 7 5 2 4 5 7 2 1 |
9 |
I. Mukofotlar
Xotira: 32 MB, Vaqt: 1000 msFan olimpiadalari markazi (FOM) nihoyat "O'qituvchilar Olimpiadasi"ni o'tkazdi! Ustozlarimiz bilimda kuch sinashib, butun Respublika bo'ylab eng zo'r o'qituvchi nomiga loyiq bo'lishdi. Hamma ishtirokchilar natijalarini intiqlik bilan kutmoqda, sababi FOM barcha qatnashchilarga alohida pul mukofoti tayyorladi! Lekin, albatta, buni ham ajoyib va adolatli tarzda amalga oshirish rejalangan:
- FOM dagi pul kupyuralari faqat \(K^0, K^1, K^2, ..., K^{\infty}\) ko'rinishida (ya'ni, K ning nomanfiy butun darajalari).
- Ustozlar bir xil qiymatdagi kupyuradan ko'pi bilan bittadan olishi mumkin va har bir ustoz hech bo'lmaganda bitta kupyura bilan taqdirlanadi.
- Eng oxirgi oʻrindagi ustoz, yaʼni \(N\)-oʻrin egalari, yuqoridagi cheklovlar asosida to'lash mumkin bo'lgan eng kichik miqdordagi mukofotni oladi. \((N-1)\)-o'rin sohibi esa undan keyingi eng kichik mukofotni, va hokazo. \(i\)-o‘rindagi ustoz \(N-i+1\)-eng kichik mukofotga ega bo‘ladi, boshqacha so'zlar bilan aytganda, eng kichik mukofot — oxirgi o‘ringa, eng katta mukofot esa 1-o‘ringa beriladi..
Misol uchun, agar \(N = 5, K = 3\) bo‘lsa:
Eng kichik hosil qilib bo‘ladigan mukofotlar: \([1, 3, 4, 9, 10]\). Demak, 1-o‘rin uchun 10 so‘m, 2-o‘rin uchun 9 so‘m, va hokazo!
Endi har bir ustoz o'z o'rnini biladi va mukofot miqdorini ham bilishni xohlaydi. Ularning hayajonini kutarib, siz tashkilotchi sifatida qo'lga kiritgan mukofotlarni aniqlab, ularga xursandchilik ulashing!
Birinchi qatorda probel bilan ajratilgan 3 ta natural son \(N, K, Q \) - ishtirokchilar soni, FOM tomonidan belgilangan kupyura birligi, hamda so'rovlar soni kiritiladi.
Keyingi \(Q\) ta qatorning har birida 1 tadan butun son - o'qituvchi egallagan o'rin kiritiladi.
\(1 \le N \le 10^9\)
\(1 < K \le 10^9\)
\(1 \le Q \le 10^5\)
Har bir so'rov uchun alohida qatorda, o'qituvchi oladigan mukofot qiymatini chop eting. Javob juda katta bo‘lishi mumkin, shu sababli natijaning \(10^9 + 7\) ga bo‘lgandagi qoldig'ini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 3 4 1 2 3 5 |
10 9 4 1 |
| 2 |
10 4 5 4 7 1 10 3 |
21 16 68 1 64 |
J. Dekart o'yini
Xotira: 32 MB, Vaqt: 1000 msHusanboy bilan Shohruh aqliy raqobat qiladigan standart o'yinlarning barchasini birgalikda juda ko'plab marotaba o'ynashgan. Shu sababli ular standart o'yinlardan zerikib qolishdi va o'zlarining aqliy raqobat qiladigan dekart o'yini nomli o'yinlarini o'ylab topishdi.
O'yin quyidagicha izohlanadi:
- O'yin ikki o'yinchi orasida o'ynaladi;
- O'yinda amal bajarishni birinchi o'yinchi (\(A\)) boshlab beradi, ikkinchi o'yinchi (\(B\)) davom ettiradi, va shu tariqa o'yinda amal bajarish navbati almashib kelaveradi. Ya'ni \(A \rightarrow B \rightarrow A \rightarrow B \rightarrow A \rightarrow ...\) ketma-ketligida;
- O'yin davomida o'yinchilarda dekart koordinatalar sistemasida joylashgan bitta o'yin toshi mavjud bo'lib bu o'yin toshining dastlabki joylashuv koordinatasi \((x_0,y_0)\) ekanligi ma'lum. Bu yerda \(x_0\) va \(y_0\) natural sonlar;
- Har bir o'yinchi o'zining amal bajarish navbati kelganida o'yin toshini ayni vaqtdagi koordinatasi \((x, y)\) dan olib, boshqa bir koordinata\((x', y')\)ga joylashtirishi kerak, bunda quyidagi shartlar bajarilishi zarur:
- \(0 \le x' \le x\)
- \(0 \le y' \le y\)
- \(x'\) va \(y'\) butun son
- \(0 < |x-x'|+|y-y'| \le k\)
- O'z navbati kelganida o'yin toshini \((0,0)\) koordinataga olib kelgan o'yinchi o'yin g'olibi hisoblanadi.
Agarda ushbu o'yinni Husanboy va Shohruh birgalikda o'ynashsa, o'yinda amal bajarishni Husanboy boshlab bersa hamda har ikkala o'yinchi optimal o'ynasa o'yinda kim g'olib bo'lishini aniqlang.
Kirish faylining birinchi satrida ikkita butun son, \(x_0\) va \(y_0\) sonlari - o'yin boshida o'yin toshi qaysi koordinatada joylashganligi kiritiladi. Ikkinchi satrda esa bitta butun son, \(k\) - o'yin toshini koordinatasini o'zgartirish uchun kiritilgan cheklov masofasi kiritiladi.
Cheklovlar: \(1 ≤ x_0, y_0, k ≤ 1000\)
Eslatma: O'yinni \(Husanboy\) boshlab beradi
Chiqish faylida yagona so'z, ikkala o'yinchi ham optimal o'yin o'ynaganda kim g'olib bo'lishini (\(Husanboy\) yoki \(Shohruh\)) chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
1 1 2 |
Husanboy |
| 2 |
1 1 1 |
Shohruh |
| 3 |
1000 1000 1000 |
Husanboy |
K. DoubleWont
Xotira: 32 MB, Vaqt: 1000 msAbdulla bayram munosabati bilan o'g'li Anvar va uning do'sti Akbarni ko'ngilochar bog'(Park)ga olib borishga qaror qildi. Bogda ba'zi bir ko'ngilochar qurilma(Atraksion)larga chiqish uchun eng kam yosh chegarasi belgilangan bo'lib, bu ko'ngilochar qurilmalarga faqatgina yoshi belgilangan yosh chegarasiga yetgan yoki undan kattalar chiqa oladi xolos. Bog'ga kirishda Abdulla barcha Atraksionlar uchun kerakli yosh chegarasini aniqlab oldi. Ma'lum bo'lishicha ularning barchasiga o'g'li Anvarning yoshi yetarli. Endi Akbarning yoshini bilish qoldi xolos.
Shu sababli Abdulla o'g'lining do'sti Akbardan yoshini so'radi. Akbar o'zining yoshini \(N\) yosh deb aytdi. Abdulla o'zining o'g'li bilan bo'lgan suhbatlardan biladiki Akbarning DoubleWont (2 barobar qilib aytish odati) bor. Endi Abdulla yosh cheklovi kamida \(M\) deb belgilangan Atraksionga Akbarni chiqarsa bo'ladimi yoki yo'q, shuni aniqlamoqchi. Buni aniqlashda Abdullaga yordam bering.
Kirish faylining dastlabki satrida bitta butun son, \(T(1 \le T \le 100)\)testlar soni kiritiladi, keyingi \(T\) ta satrda har bir test uchun ikkita butun son, \(N\) va \(M (0 < N, M \le 30)\) sonlari kiritiladi.
Har bir test uchun alohida satrda, agar Akbar yosh cheklovi kamida \(M\) deb belgilangan Atraksionga chiqa olsa Yes, aks holda No so'zini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
5 12 20 12 5 12 12 12 6 12 7 |
No Yes No Yes No |
L. Xeshlash
Xotira: 32 MB, Vaqt: 1000 msKamol kompyuteriga parol o'ylab topganda parolni unutib qo'yish odati ham bor. Shu sababli u kompyuteriga murakkab parol qo'ymaydi, uning o'rniga \([0, 46]\) oralig'idagi sonlardan birini qo'yadi. Unutib qo'ygan taqdirda har bir sonni tekshirib ko'rish Kamol uchun unchalar qiyin emas.
Agarda Kamol kompyuterga parol qo'ymoqchi bo'lgan vaqtda biror bir so'zni tanlasa, kompyuterga parol sifatida shu so'zning Xeshlangan qiymatini qo'yadi.
Albatta satrlarni Xeshlashning juda ko'plab turlari mavjud, Kamol esa satrni Xeshlangan qiymati \([0,46]\) oralig'iga mos kelishi uchun satrdagi har bir harfning alfabetdagi tartib raqamlari ko'paytmasini 47 ga bo'lgandagi qoldiqdan foydalanadi.
Hozirgi vaqtda Kamol kompyuteri uchun \(A\) satrni parol sifatida tanlagan. Ammo tanlagan satrini unutib qo'ygan. Hozirda u parol sifatida tanlagan satri \(B\) deb o'ylamoqda.
Siz Kamol hozir kompyuterni bir urinishda ocha oladimi yoki yo'q, shuni aniqlashingiz kerak.
Kirish faylida alohida qatorda ikkita satr, \(A (1 \le |A| \le 6)\) va \(B (1 \le |B| \le 6)\) satrlari kiritiladi.
\(A\) satri va \(B\) satrining Xesh qiymati bir xil bo'lsa Welcome, aks holda Try again yozuvini chop eting!.
1-test:
KAMOLA: \((11 \times 1 \times 13 \times 15 \times 12 \times 1) \ mod \ 47 = 25740 \ mod \ 47 = 31\)
KAMOL: \((11 \times 1 \times 13 \times 15 \times 12) \ mod \ 47 = 25740 \ mod \ 47 = 31\)
2-test:
BY: \((2 \times 25) \ mod \ 47 = 50 \ mod \ 47=3\)
AC: \((1 \times 3) \ mod \ 47 = 3 \ mod \ 47 = 3\)
3-test:
ROBO: \((18 \times 15 \times 2 \times 15) \ mod \ 47 = 16\)
NUMBER: \((14 \times 21 \times 13 \times 2 \times 5 \times 18) \ mod \ 47 = 21\)
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
KAMOLA KAMOL |
Welcome |
| 2 |
BY AC |
Welcome |
| 3 |
ROBO NUMBER |
Try again |
| 4 |
BOBIR DORI |
Welcome |
M. Nomofobiya
Xotira: 32 MB, Vaqt: 1000 msBarchaga ma'lumki yosh avlod uchun raqamli aloqa hayotning ajralmas qismi bo'lishga allaqachon ulgurdi. Hozirda biror bir o'smirning uyali telefonini olib qo'yish unda kuchli stress uyg'otishi mumkin.
Davron ixtisoslashtirilgan maktabda o'qituvchi bo'lib ishlaydi, va u o'quvchilar dars vaqtida telefonga chalg'imasligi uchun quyidagi qarorga keldi: dars jarayonida har bir telefon bilan bog'liq qoidabuzarlik uchun o'quvchilar jarima ballari to'plashadi. Agar o'quvchining yig'gan jarima bali 100 ga yetsa hafta oxirida (ya'ni dam olish kunida) uning telefoni olib qo'yiladi. Jarima ballari har bir hafta uchun alohida hisoblanadi, ya'ni eski haftada yig'ilgan jarima ballari yangi haftaga ko'chib o'tmaydi.
Shunday qilib u o'zining dars o'tadigan sinflariga quyidagi jadvalni e'lon qildi:
| Qoidabuzarlik turi | Kod | Jarima bali |
| Telefondan foydalanish haqida bahslashish | FB | 25 |
| Sms qabul qilish | SQ | 30 |
| Mashg'ulotlar vaqtida Sms yozish | MS | 50 |
| Suratga olish | SO | 60 |
| O'qituvchi gapirayotganda sms yozish | GS | 75 |
| Telefon jiringlashi | TJ | 80 |
Bu ma'lumotlar o'quvchilarga e'lon qilinganidan so'ng Davron har bir hafta uchun alohida qog'ozda haftaning tartib raqamini hamda o'quvchilarning qoidabuzarlik qilish ketma-ketligini o'quvchining ismi va qoidabuzarlik kodi shaklida yozib qo'yishni odat qildi, bu esa unga hafta oxirida o'quvchilarning jarima ballarini hisoblashida va 100 bal yoki undan yuqori bal yig'gan o'quvchilarni jazolashda yordam beradi.
Bugun Davron har bir hafta davomida yozib olingan qog'ozlarini hamkasbi(ya'ni siz)ga ko'rsatmoqda. Siz keltirilgan qaydlardan foydalanib har bir haftada kimlar jazolanganligini aniqlashingiz kerak.
Kirish ma'lumotlarida bir nechta hafta haqida so'rovlar bo'lishi mumkin. So'rovlar soni 50 tadan ko'p emasligi kafolatlanadi.
Har bir so'rov uchun:
- Dastlabki satrda ikkita butun son, \(N (0 < N \le 50)\) va \(M (0 < M \le 50)\) sonlari kiritiladi. Bu yerda \(N\) - haftaning tartib raqamini, \(M\) esa shu haftada nechta qoidabuzarlik holati qayd etilganligini anglatadi.
- Keyingi \(M\) ta qatorda ikkitadan so'z, qoidabuzarlik qilgan o'quvchining ismi hamda qoidabuzarlik kodi kiritiladi.
Har bir so'rov uchun natijani alohida satrda chop eting.
Natijani chop etish dastlab hafta tartib raqami bilan, ya'ni N-hafta bilan boshlanishi kerak. Shundan so'ng agarda shu haftada hech qanday jazo qo'llanilmagan bo'lsa "Hech kimning telefoni olib qo'yilmadi" so'zini, aks holda telefoni olib qo'yilgan o'quvchilarning ismini vergul bilan ajratgan holda, ismlarning qaydnomada birinchi uchrashi tartibini saqlab qolgan holda chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
3 7 Shohruh GS Zaynab SQ Eldor MS Eldor MS Shohruh SQ Zaynab FB Zaynab SQ 1 3 Zaynab FB Zaynab SQ Zaynab SQ 2 7 Eldor MS Shohruh GS Zaynab SQ Eldor MS Shohruh SQ Zaynab FB Zaynab SQ |
3-hafta Shohruh, Eldor 1-hafta Hech kimning telefoni olib qo'yilmadi 2-hafta Eldor, Shohruh |
N. Nihoyatda farovon hayot
Xotira: 32 MB, Vaqt: 1000 msUzoq-uzoqlarda bir sayyorada N ta mamlakat mavjud. Bu sayyoradagi ba’zi mamlakatlar o‘rtasida hamkorlik shartnomasi tuzilgan.
Sayyorada iqtisodiy qonun qat’iy:
- Agar ikki mamlakat hamkor bo‘lsa, bir mamlakatning aholisi ikkinchi mamlakatning mahsulotini sotib olsa undan hech qanday boj olinmaydi.
- Agar ikki mamlakat hamkor emas bo‘lsa, bir mamlakatning aholisi ikkinchi mamlakatning mahsulotini sotib olsa undan 500 foiz boj olinadi.
Shu sababdan, agar bir kun kelib barcha mamlakatlar o‘zaro hamkor bo‘lsa, bojlar butunlay yo‘qoladi va sayyora aholisi nihoyatda farovon hayot kechiradi.
Bu sayyorada yashovchi qadimiy Sehrgar o‘zining noodatiy sehr kuchi bilan mamlakatlar o‘rtasidagi hamkorlikni o‘zgartirish qobiliyatiga ega, ya'ni:
- Sehrgar bitta mamlakatni tanlaydi.
- Tanlangan mamlakat bilan ilgari hamkor bo‘lganlarning barchasi endi hamkor emas.
- Aksincha, ilgari hamkor emas bo'lganlarning barchasi endi hamkor bo‘lib qoladi.
Ya’ni, tanlangan mamlakat boshqa barcha mamlakatlarga nisbatan “teskari” holatga o‘tadi.
Savol shuki: Sehrgarning mohirona tanlovlari natijasida, qachondir sayyora aholisi nihoyatda farovon hayot kechiradimi?
Birinchi qatorda bitta butun son N (2 ≤ N ≤ 1000) — mamlakatlar soni.
Masalani osonlashtirish maqsadida mamlakatlar 1 dan N gacha bo'lgan sonlar bilan raqamlangan.
Ikkinchi qatorda bitta butun son M (0 ≤ M < N·(N−1)/2) — hozirgi vaqtda mavjud bo‘lgan hamkorlik shartnomalari soni.
Keyingi M ta qatorda ikkita turli butun son — hamkorlik qilayotgan mamlakatlar raqamlari beriladi.
Agar Sehrgarning mohirona tanlovlari natijasida, qachondir sayyora aholisi nihoyatda farovon hayot kechira olsa HA so'zini, aks holda YO'Q so'zini chop eting.
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 0 |
HA |
| 2 |
3 2 1 3 2 3 |
YO'Q |
| 3 |
4 2 2 3 1 4 |
HA |
| 4 |
3 1 2 3 |
HA |
O. IDTK
Xotira: 32 MB, Vaqt: 2000 msBitboy IDTK(Ikkining Darajalaridan Tuzilgan Ketma-ketlik)ni juda yaxshi ko'radi. Uning tug'ilgan kuniga otasi Baytboy \(2^N\) sonini sovg'a qildi. Bu sonni Bitboy o'zi uchun tuzmoqchi bo'lgan IDTK ning dastlabki (va hozircha yagona) elementi qilib oldi.
Bitboy ixtiyoriy vaqtda o'zining IDTKi ichiga quyidagicha o'zgartirish kiritishi mumkin:
- IDTK ichidan qiymati \(K (K > 1)\) ga teng bo'lgan ixtiyoriy sonni tanlab uning o'rniga shu sonni ikkiga bo'lingan qiymatidan 2 ta ya'ni \(K/2\), \(K/2\) ni joylashtirishi mumkin.
- IDTK ichidan qiymati \(K (K > 2)\) ga teng bo'lgan ixtiyoriy sonni tanlab uning o'rniga\(K/4\), \(K/2\), \(K/4\) ni joylashtirishi mumkin.
Shuni esda saqlash kerakki, Bitboy IDTK dagi qiymatlarning o'rnini o'zgartira olmaydi.
Bitboyning odatlarini juda yaxshi bilgan Baytboy o'g'liga bergan \(2^N\) soni oradan vaqtlar o'tib qanday ketma-ketlik bo'lishi mumkinligi haqida qiziqib qoldi. O'ylab qarasa bo'lishi mumkin bo'lgan ketma-ketliklar soni juda ko'p ekan. Shu sababli u bo'lishi mumkin bo'lgan ketma-ketliklar sonini topmoqchi. Unga buni aniqlashda yordam bering.
Kirish faylida yagona butun son, \(N(0 \le N \le 10^7)\) soni kiritiladi.
Baytboy aniqlamoqchi bo'lgan qiymatni \(10^9 + 9\) ga bo'lgandagi qoldiqni chop eting.
1-test:
\(N=2\)
Baytboy sovg'a qilgan son \(2^N=2^2=4\)
| yakuniy holat | Kelib chiqish bosqichlari | |
| 1 | [4] | [4] |
| 2 | [2,2] | [4]->[2,2] |
| 3 | [1,1,2] | [4]->[2,2]->[1,1,2] |
| 4 | [2,1,1] | [4]->[2,2]->[2,1,1] |
| 5 | [1,2,1] | [4]->[1,2,1] |
| 6 | [1,1,1,1] | [4]->[2,2]->[1,1,2]->[1,1,1,1] |
| [4]->[2,2]->[2,1,1]->[1,1,1,1] | ||
| [4]->[1,2,1]->[1,1,1,1] |
| # | INPUT.TXT | OUTPUT.TXT |
|---|---|---|
| 1 |
2 |
6 |
| 2 |
4 |
2350 |