Masala E
Statistika - 1
Sizga \( n \) uzunlikdagi \( X \) massivi berilgan. Har bir element \( x_i \) nuqtani ifodalaydi. Siz ikkita turdagi so'rovlarni bajarishingiz kerak:
1. \( 1 \ i \ a \): Bu so'rovda \( x_i \) qiymatini \( a \) ga o'zgartirish kerak bo'ladi.
2. \( 2 \ l \ r \): Bu turdagi so'rovda massivning \( [l, r] \) oralig'idagi nuqtalarning populyatsiya standart chetlanishini hisoblash kerak bo'ladi.
Populyatsiya standart chetlanishi \( \sigma \) quyidagi formula bilan hisoblanadi:
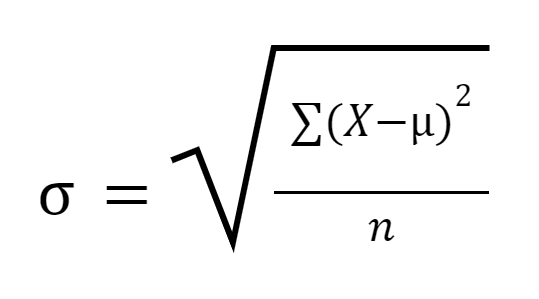
Bu yerda:
- \( \mu = \frac{\sum x_i}{n} \) , ya'ni \( x_i \) larning o'rta arifmetik qiymati.
- \( n \) — oraligdagi nuqtalar soni.
Birinchi qatorda ikkita butun son \( n \) va \( q \) berilgan, bunda:
- \( n \) — massiv uzunligi.
- \( q \) — so'rovlar soni.
Ikkinchi qatorda \( n \) ta butun son \( x_i \) berilgan, massiv elementlarini ifodalaydi.
Keyingi \( q \) qatorda so'rovlar berilgan:
- Yangilash So'rovi uchun qatorda \(1 \ i \ a\) berilgan, bunda:
- \( i \) — yangilanadigan element indeksi (indekslash 1 dan boshlangan deb hisoblanadi).
- \( a \) — \( x_i \) ning yangi qiymati.
- Oraliq So'rovi uchun qatorda \(2 \ l \ r\) berilgan, bunda:
- \( l \) va \( r \) — \( [l, r] \) oralig'ining indekslari (indekslash 1 dan boshlangan deb hisoblanadi).
Qiymat chegaralari:
- \( 1 \leq n, q \leq 10^5 \)
- \( -25 \leq x_i, a \leq 25 \)
- \( 1 \leq i, l, r \leq n \)
Har bir oraliq so'rovi uchun \( [l, r] \) oralig'idagi nuqtalarning populyatsiya standart chetlanishini chiqaring. Natijani 6 kasr belgigacha yaxlitlab chiqaring.
| # | input.txt | output.txt |
|---|---|---|
| 1 |
5 3 1 2 3 4 5 2 1 5 1 3 10 2 1 5 |
1.41421356 3.13687743 |
| 2 |
3 2 -1 0 1 2 1 3 1 2 5 |
0.81649658 |
formuladagi \(n\) massiv uzunligi emas!. Formuladagi \(n\) nima ekanligi formulani pastida yozilgan!
